A constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1 Find ∂z ∂x and ∂z ∂y for each of the following functions (Click on the green letters for solutions) (a) z = x2y4, (b) z = (x4 x2)y3, (c) z = y12 sin(x)Variable twhereas uis a function of both xand y 2 Chain rule for two sets of independent variables If u = u(x,y) and the two independent variables x,y are each a function of two new independent variables s,tthen we want relations between their partial derivatives 1 When u = u(x,y), for guidance in working out the chain rule, write down the(i) y =x2 2xz z2 x z x y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ x y 2 2 = ∂ ∂ ∂ x z y x z z y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ z y 2 2 = ∂∂ ∂ z x y (ii) y =x2 z2 3z 2xz2 x y = ∂ ∂ 2 2 2 2z x y = ∂ ∂ xz x z y 4 2 = ∂ ∂ ∂ =2 2 3 ∂ ∂ x z z y 2 2 2 2x z y = ∂ ∂ xz z x y 4 2 = ∂∂ ∂ (iii) = =xz−1 z x y z z x y 1 1 = = ∂ ∂ − 0 2 2 = ∂ ∂ x y 2 2 2 1 z z x z y =− =− ∂ ∂ ∂ − 2 2 z x xz z y =− =− ∂ ∂ − 3 3 2 2 2 2 z x xz z y = = ∂ ∂
If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community
Partial derivative of log(x^2 y^2)^1/2
Partial derivative of log(x^2 y^2)^1/2-Click here👆to get an answer to your question ️ If u = log (x^2y^2z^2), verify ∂^2u∂x ∂y = ∂^2u∂x ∂y Join / Login >> Class 12 >> Maths Oscillations Redox Reactions Limits and Derivatives Motion in a Plane Mechanical Properties of Fluids class 12Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2x



Rules Of Calculus Multivariate
PARTIAL DERIVATIVES AND THEIR APPLICATIONS 4 aaaaa 41 INTRODUCTON FUNCTIONS OF SEVERAL VARIABLES So far, we had discussed functions of a single real variable defined by y = f(x)Here in this chapter, we extend the concept of functions of two or more variablesThe partial derivative of y = f(x) with respect to x is written as f x x,y , or z x y y y y e y y e y y f x y 1 1 ln 1 3 1 3 2 3 2 2 Example 5 Find f z if , 35 1 yz2 z f y zx w means we act as if z is our only variable, so we'll act as if all the other variables (x, y and w) I am new to partial derivatives and they seem pretty easy, but I am having trouble with this one $$\frac{\partial}{\partial x} \ln(x^2y^2)$$ now if this was just $\frac{d}{dx}\ln(x^2)$ we would get $\frac{2x}{x^2}$ So I feel we would get$$\frac{\partial}{\partial x} \ln(x^2y^2)=\frac{2x}{x^2y^2}$$
Section 22 Partial Derivatives For problems 1 – 13 find all the 1st order partial derivatives \(f\left( {x,y,z} \right) = {x^3}\sqrt y 4{z^3}{y^2} xyz {xAnswer f x = y sec 2 (xy) cos x and f y = x sec 2 (xy) Question 2 If f(x,y) = 2x 3y, where x = t and y = t 2 Derivative f with respect to t Solution We know, d f d t = ∂ f ∂ x d x d t ∂ f ∂ y d y d t \frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} \frac{\partial f}{\partial y}\frac{dy}{dt} d t d f = ∂ x ∂ f d t d x ∂ y ∂ f d t d y I have a function g as a function of x;
Logarithmic differentiation Calculator online with solution and steps Detailed step by step solutions to your Logarithmic differentiation problems online with our math solver and calculator Solved exercises of Logarithmic differentiationFx(x,y) = (3x2y − y3)/(x2 y2) − 2x(x3y − xy3)/(x2y2)2, f x(0,y) = −y, fxy(0,0) = −1, fy(x,y) = (x3 − 3xy2)/(x2 y2) − 2y(x3y − xy3)/(x2 y2)2, f y(x,0) = x, fy,x(0,0) = 1 An equation for an unknown function f(x,y) which involves partial derivatives with respect to at least two different variables is called a partial differential equation3 If z = f(x) for some function f(), then –z = jf0(x)j–x We will justify rule 1 later The justification is easy as soon as we decide on a mathematical definition of



14 3 Partial Differentiation



Partial Derivatives
Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 2 n = 2 Since y 2 y 2 is constant with respect to x x, the derivative of y 2 y 2 with respect to x x is 0 0 Combine fractions Tap for more steps Add 2 x 2 x and 0 0 Combine 2 2 and 1 x 2 y 2 1 x 2 y 2Holds, then y is implicitly defined as a function of x The partial derivatives of y with respect to x 1 and x 2, are given by the ratio of the partial derivatives of F, or ∂y ∂x i = − F x i F y i =1,2 To apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total211 Partial Derivatives of First Order Consider a function z = f (x, y) of two independent variables x and y By keeping y as a constant and varying x only, z becomes a function of x alone The derivative of z with respect to x (y is kept constant) is called the




Finding The Derivative Of Log X Video Lesson Transcript Study Com




Chapter 5 Partial Differentiation Chapter 5 Partial Differentiation
Basic partial derivatives u = log( $x^2$ $y^2$ ), prove $ \frac{\partial^2 \;I want to take derivative of g with respect to ln x, ie dg/d ln x where g= ax^2/(1ax^2/r^2) Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other




Natural Logarithm Wikipedia




Diploma Engineering Mathematics Notes
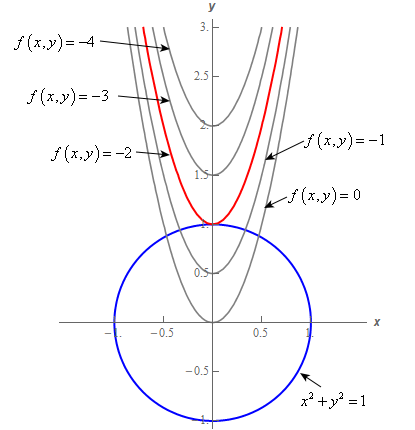
Explanation d dx (√x) = 1 2√x, so d dx (√u) = 1 2√u du dx d dx (√x2 y2) = 1 2√x2 y2 ⋅ d dx (x2 y2) = 1 2√x2 y2 (2x 2y dy dx) = 1 2√x2 y2 2x 1 2√x2 y2 2y dy dx = x √x2 y2 y √x2 y2 dy dx In order to solve for dy dx you will, of course, need the rest of the derivative of the rest of the original equation Answer link2 Partial Differentiation 2A Functions and Partial Derivatives 2A1 In the pictures below, not all of the level curves are labeled In (c) and (d), theExercise Week 9_solutionspdf EXERCISES WEEK 9 Exercise(1 Find the first partial derivatives of(1 f(x y = y 5 − 3xy(2 f(r s = r log(r2 s2 xy 2(3




Solved 4 Find And Simplify All Second Order Partial Chegg Com




Find Nth Derivative Of Log X 2 A 2 Brainly In
As a secondorder differential operator, the Laplace operator maps C k functions to C k−2 functions for k ≥ 2The expression (or equivalently ()) defines an operator Δ C k (R n) → C k−2 (R n), or more generally, an operator Δ C k (Ω) → C k−2 (Ω) for any open set ΩMotivation Diffusion In the physical theory of diffusion, the Laplace operator (via Laplace's equationI'm familiar with the derivative of log x but not when x is raised to a power or when y is involved Could someone offer some help?U'=xy^(x1) Partial derivatives are the differentiation of implicitfunction with respect to a single variable treating the other variable as a constant The consideration of a constant is decided with respect to the variable we differentiate A function of the form f(x,y)=c where c is a constant Then f is said to be a implicit function



12 3 Partial Derivatives Mathematics Libretexts




Implicit Differentiation Advanced Example Video Khan Academy
Derivative of arctanx at x=0Any suggestions would be really appreciatedSection 3 Directional Derivatives 8 Quiz Select a point from the answers below at which the scalar field f(x,y,z) = x2yz −xy2z decreases in the y direction (a) (1,−1,2), (b) (1,1,1),




How To Calculate Fxy Partial Derivatives




Max And Min X Y Ln X 2 Y 2 Mathematics Stack Exchange
Separable differential equations Calculator online with solution and steps Detailed step by step solutions to your Separable differential equations problems online with our math solver and calculator Solved exercises of Separable differential equationsAnswer (1 of 2) There is no such thing as the "derivative of f(x)" There is always, even if only implicitly, a variable that the derivative is in respect to So, properly, you have to refer to the "derivative of f(x) with respect to x" In the case of f(x), it is common to just assume that it iAnd if you know of a website that fully explains this please let me know Thanks




Derivative Of X 2 Y 2 Log Xy Youtube




Derivative Rules
Second derivative of sin^2;Rules for finding partial derivatives Let z = f(x,y) 1 To find ∂f ∂x, regard y as a constant and differen tiate f with respect to x 2 To find ∂f ∂y, regard x as a constant and differen tiate f with respect to y ExampleSo in the last couple videos I talked about partial derivatives of multivariable functions and here I want to talk about second partial derivatives so I'm going to write some kind of multivariable function let's say it's I don't know sine of X times y squared sine of X multiplied by Y squared and if you take the partial derivative you have two options given that there's two variables you can



2



2
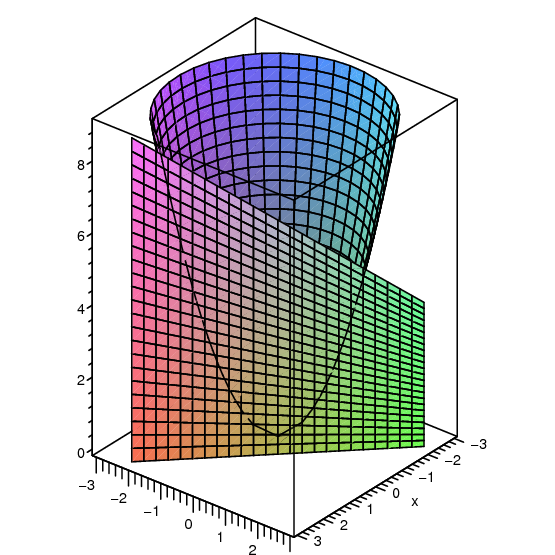
A partial derivative of a multivariable function is the rate of change of a variable while holding the other variables constant For a function z = f ( x, y), {\displaystyle z=f (x,y),} we can take the partial derivative with respect to either x {\displaystyle x} orFree partial derivative calculator partial differentiation solver stepbystepImplicit Equations and Partial Derivatives z = p 1 x2 y2 gives z = f (x, y) explicitly x2 y2 z2 = 1 gives z in terms of x and y implicitly For each x, y, one can solve for the value(s) of z where it holds sin(xyz) = x 2y 3z cannot be solved explicitly for z Prof Tesler 31 Iterated Partial Derivatives Math C / Fall 18 14 / 19




Natural Logarithm Wikipedia




Ex 5 7 9 Find Second Order Derivatives Of Log Log X
Where the three partial derivatives f x, f y, f z are the formal partial derivatives, ie, the derivatives calculated as if x, y, z were independent ∂w Example 2 Find , where w = x3y −z2t and xy = zt ∂y x,t Solution 1 Using the chain rule and the two equations in the problem, we have ∂w ∂z x = x 3 −2zt = x 3 −2zt = x 3 −2zx For implicit differentiation, we have both variables (x and y) into the derivative at once, while for partial differentiation we work with each one separately Implicitly differetiating, then, we must resort to chain rule, by naming u=x^2y^2 and, therefore, considering our original funcion z=ln(u) How can I take $\partial/\partial \theta \log L $ when $\ X$ is $ N(\mu,\sigma^2) $ Do I have to consider GLM approach?




Solved Find All The Second Order Partial Derivatives Of The Chegg Com



1
Answer to Find the secondorder partial derivatives of the function f(x, y) = ln(1 x^2 y^2) By signing up, you'll get thousands ofU}{\partial y \partial x} $Derivative of 1/ (x^2) full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge




12th Maths 1 Pdf Pages 101 150 Flip Pdf Download Fliphtml5



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community
Thus, we have 1 / (xln(e)) = 1 / (x⋅1) = 1 / x As stated in our facts, we get that the derivative of ln( x ) is 1/ x , and we see just how useful this formula can be01 Recall ordinary derivatives If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change withDerivatives of logarithmic functions are mainly based on the chain ruleHowever, we can generalize it for any differentiable function with a logarithmic function The differentiation of log is only under the base e, e, e, but we can differentiate under other bases, too




12th Maths 1 Pdf Pages 101 150 Flip Pdf Download Fliphtml5



Implicit Differentiation
Learn How to Find the First Order Partial Derivatives of f (x, y) = ln (xy^3) with Log Properties Learn How to Find the First Order Partial Derivatives of f (x, y) = ln (xy^3) with LogU}{\partial x \partial y} \;Derivatives » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for a derivative derivative of arcsin;



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Partial Derivative Math Videos Maths Exam
Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution Derivative of log(x^2y^3) ???In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant Partial derivatives are used in vector calculus and differential geometry The partial derivative of a function f {\displaystyle f} with respect to the variable x {\displaystyle x} is variously denoted by f x ′ {\displaystyle f'_{x}}, f x



Calculus Iii Lagrange Multipliers




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1
Derivative of the Logarithm Function y = ln x The derivative of the logarithmic function y = ln x is given by d d x ( ln x) = 1 x \displaystyle\frac {d} { { {\left {d} {x}\right}}} {\left ( \ln {\ } {x}\right)}=\frac {1} { {x}} dxd (ln x) = x1 You will see it written in a few other ways as wellDerivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;



2
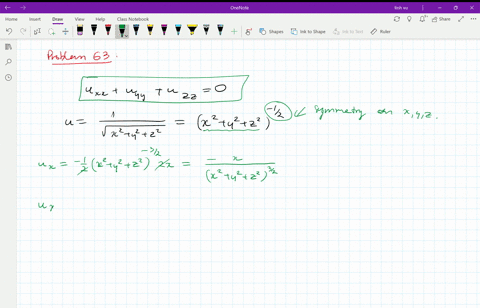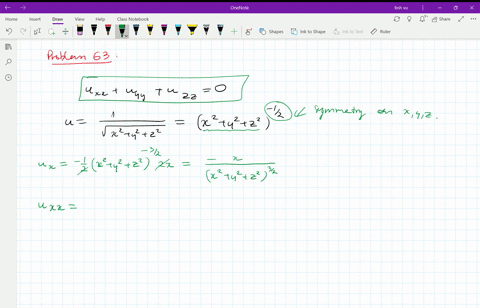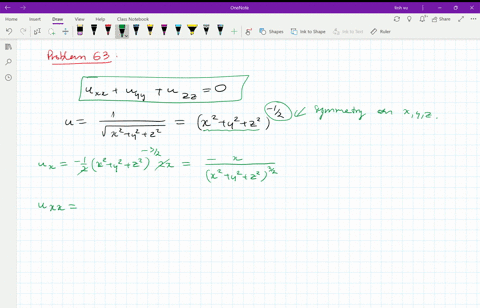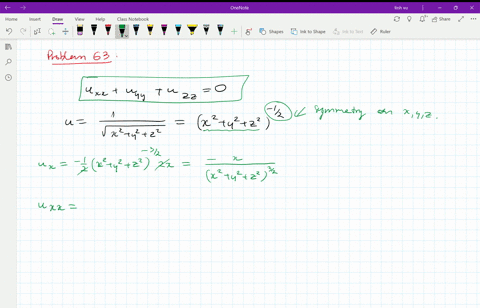



Solved Verify That The Function U 1 Sqrt X 2 Y 2 Z 2 Is A Solution Of The Three Dimensional Laplace Equation U X X U Y Y U Z Z 0



5 Derivative Of The Logarithmic Function




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube




Differentiate Log X 2 Sqrt X 2 4x 1 With Respect To X
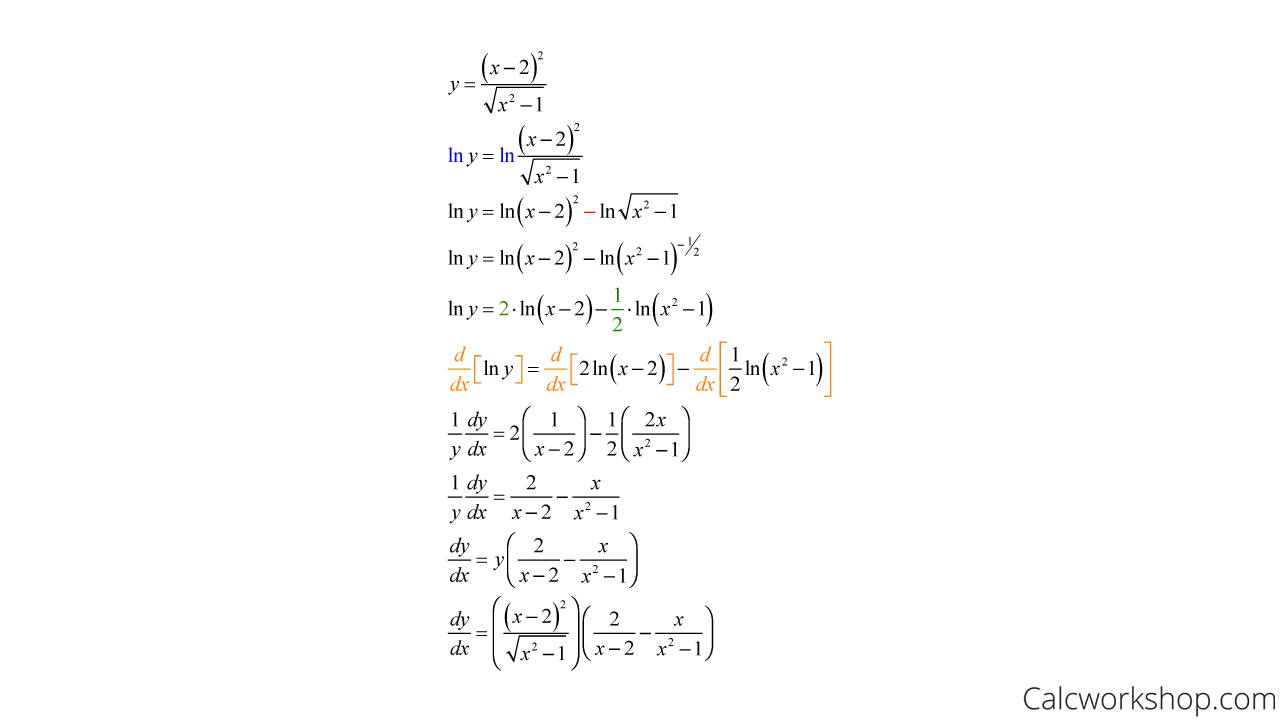



Logarithmic Differentiation W 7 Step By Step Examples



Rules Of Calculus Multivariate



What Is The Nth Derivative Of Logx Quora



Rules Of Calculus Multivariate
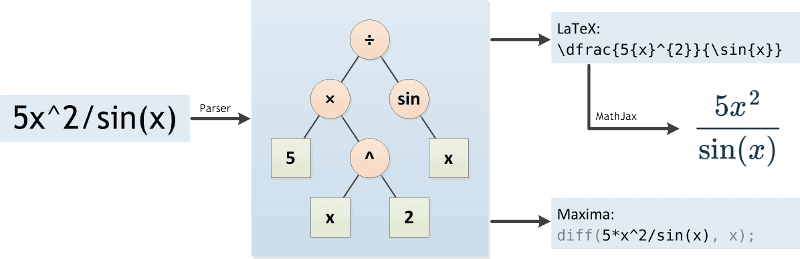



Derivative Calculator With Steps




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




Finding The Derivative Of Log X Video Lesson Transcript Study Com




Derivative Calculator Wolfram Alpha




Derivative Of Log Confusion Mathematics Stack Exchange




Ma121 Homework 8 Solutions Compute The Partial Derivatives F 1




Mathematics Ii Tranquileducation



Finding The Derivative Of Log X Video Lesson Transcript Study Com



1




2 3 Tangent Plane To A Surface Mathematics Libretexts




Diploma Engineering Mathematics Notes




Implicit Differentiation Advanced Example Video Khan Academy




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1
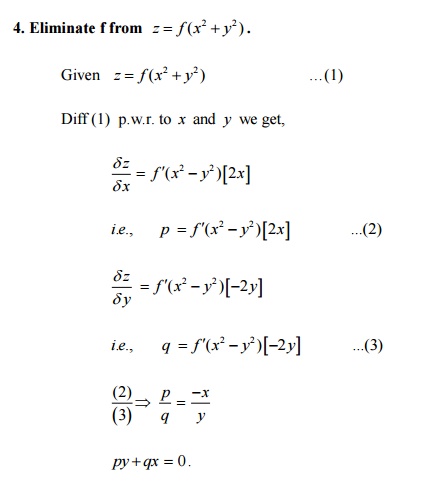



Important Questions And Answers Partial Differential Equations




Ex 5 7 9 Find Second Order Derivatives Of Log Log X



2




Derivative Of Log Confusion Mathematics Stack Exchange




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




Ex 9 2 7 Verify Solution Xy Log Y C Y Y2 1 Xy
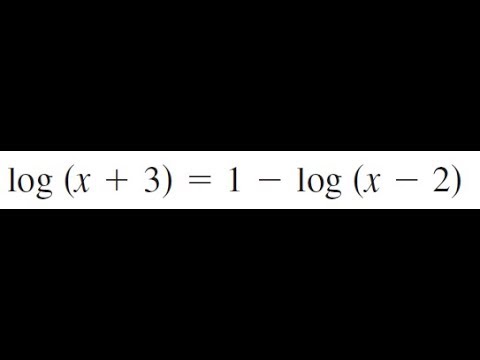



Log39x4 Log 3 3x 2 Detailed Login Instructions Loginnote
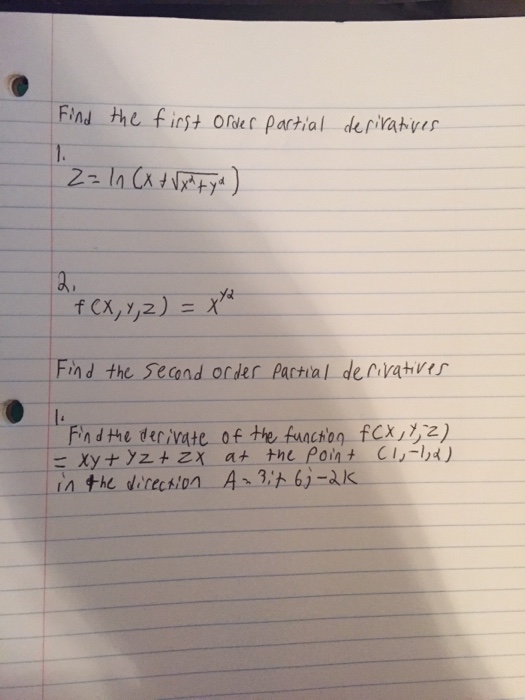



Solved Find The First Order Partial Derivatives Z Ln X Chegg Com




Wolfram Alpha Examples Step By Step Solutions




12th Maths 1 Pdf Pages 101 150 Flip Pdf Download Fliphtml5



2



2




Derivative Of Log X Sqrt X 2 A 2 W R T X Is Youtube




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y
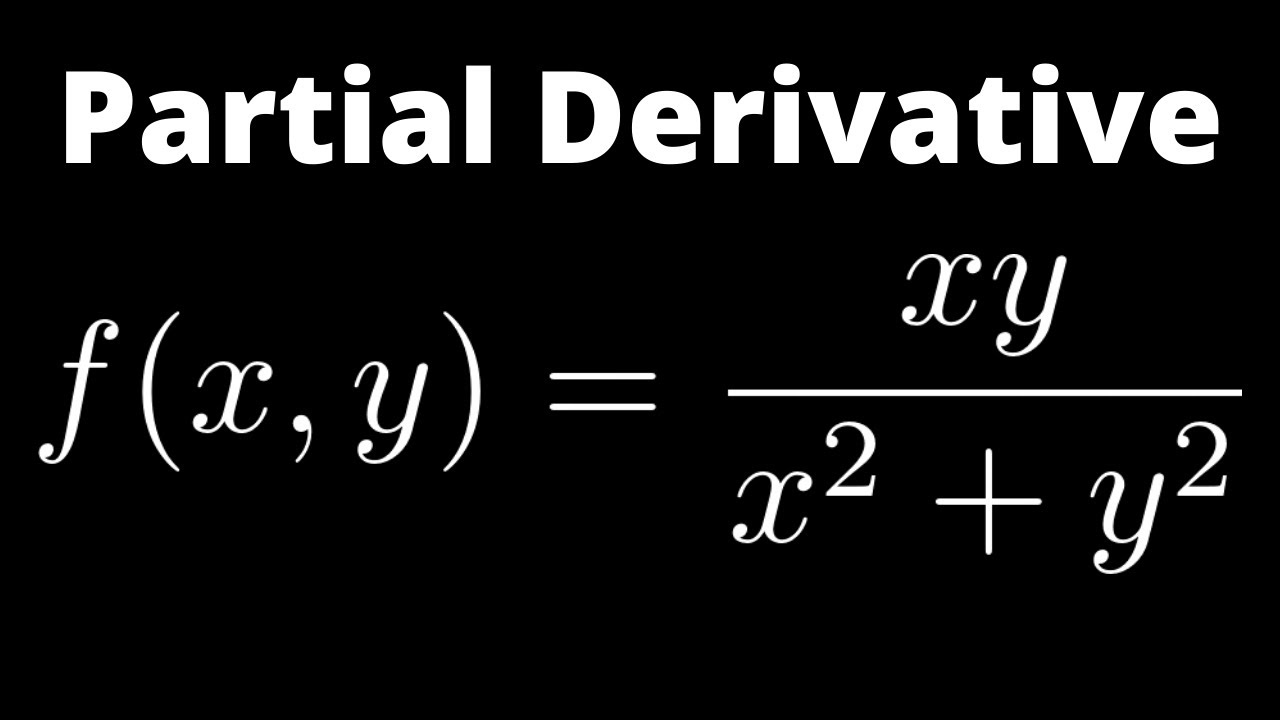



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube




Partial Derivative Examples Math Insight




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange



1
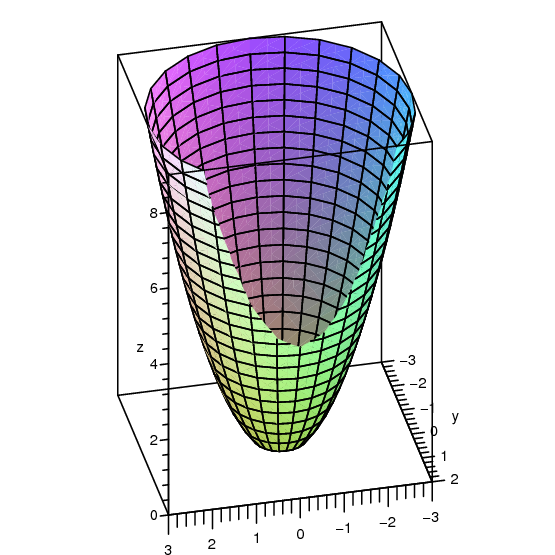



14 3 Partial Differentiation



What Is The Derivative Of E Logx Quora



Implicit And Logarithmic Differentiation




How To Do Implicit Differentiation 7 Steps With Pictures



What Is The Integration Of Log 1 X 2 Quora
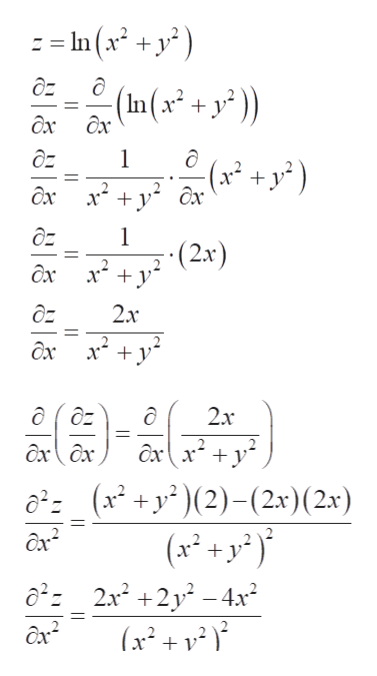



Answered Show That F X Y Ln X2 Y2 Solves Bartleby
.gif)



Calculus Differentials And Integrals



2




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu



What Is The Partial Derivative Of U Y X W R T To X And Y Quora
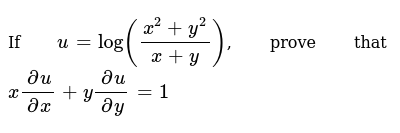



If U Log X 2 Y 2 X Y Prove That X Delu Delx Y Delu Dely 1




For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video




Partial Derivative Examples Math Insight




Solved Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Engineering Mathematics Total Derivatives Chain Rule And Derivativ
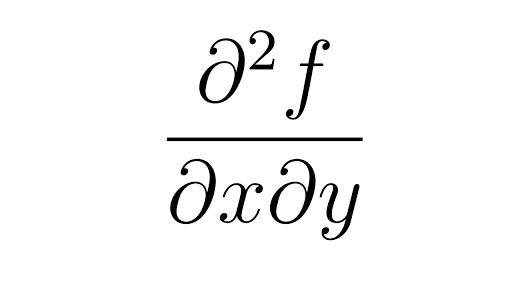



Second Partial Derivatives Article Khan Academy




Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube
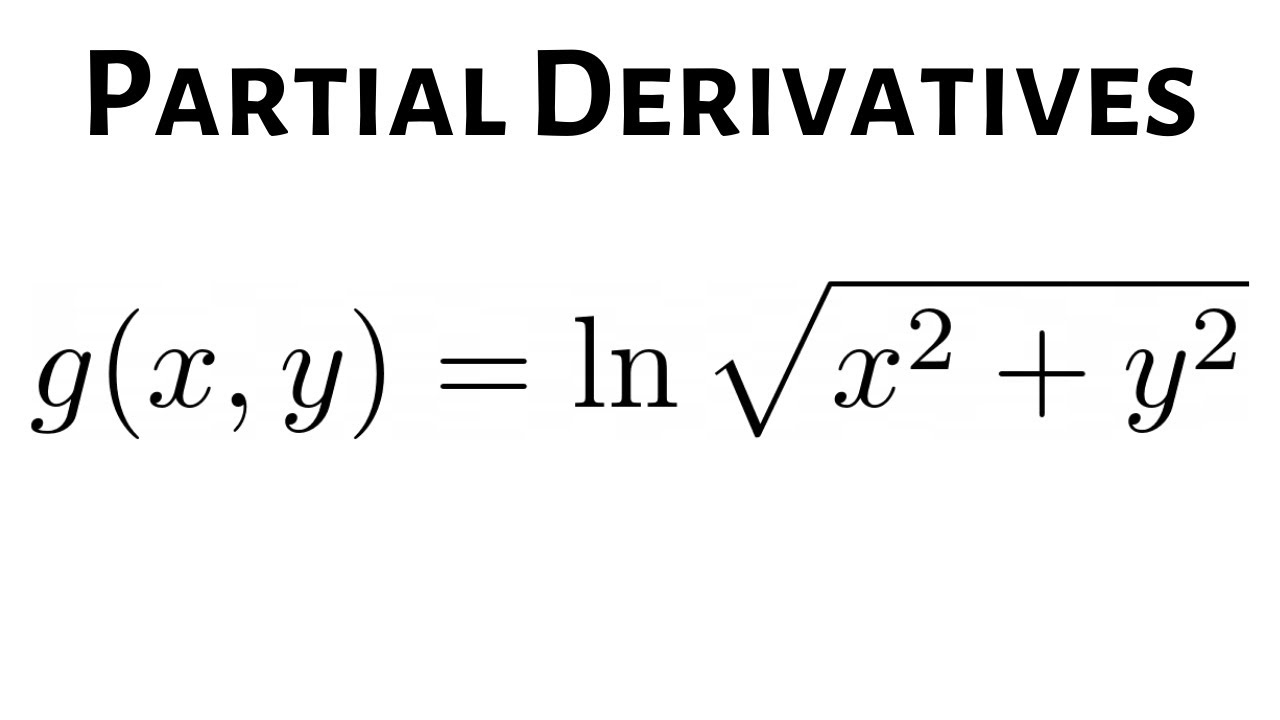



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube




Answered Find The Partial Derivatives With Bartleby




14 2 Limits And Continuity




Natural Logarithm Wikipedia



5 Derivative Of The Logarithmic Function




Derivative Of Logₐx For Any Positive Base A 1 Video Khan Academy




Verify Jj 1 Given X E U Cos V Y E U Sin V Mathematics Stack Exchange




For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video




21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube
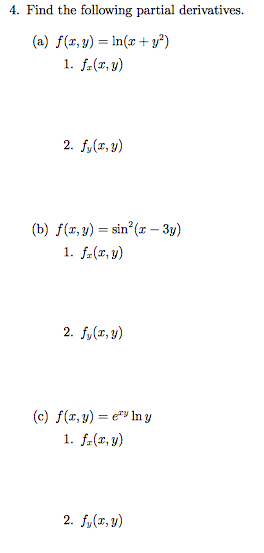



Solved 4 Find The Following Partial Derivatives A Chegg Com



Implicit And Logarithmic Differentiation




Logarithmic Differentiation W 7 Step By Step Examples




Review And Unification Of Methods For Computing Derivatives Of Multidisciplinary Computational Models Aiaa Journal



2




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube



2



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community




Implicit And Logarithmic Differentiation



0 件のコメント:
コメントを投稿